Analysis for Applications I (MATH 641)
Review of preliminary concepts
– Normed linear spaces and inner product spaces
– Subspaces, orthogonal complements, Gram-Schmidt procedure, projection operator
– Self-adjoint matrices and their properties, eigenvalue estimates: Rayleigh-Ritz maximum principle and Courant-Fischer Minimax Theorem
Banach and Hilbert spaces
– Convergent sequence, Cauchy sequence, completeness
– Lebesgue measure and integral, measurable functions, Monotone and Dominated Convergence Theorems
– Special (complete) spaces: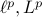 for
for 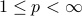 ,
, ![C^k [a,b]](eqs/711554236-130.png) , Sobolev space
, Sobolev space ![mathcal{H}^n [a,b]](eqs/1695453592-130.png) , Sobolev-type inequalities
, Sobolev-type inequalities
–![C[a,b]](eqs/1812834960-130.png) and its properties: modulus of continuity, density of splines, density of polynomials in
and its properties: modulus of continuity, density of splines, density of polynomials in ![C[a,b]](eqs/1812834960-130.png) (Weierstrass Approximation Theorem), density of
(Weierstrass Approximation Theorem), density of
polynomials in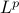 for
for 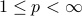
– Hilbert spaces: least-square minimization (discrete and continuous), normal equations, Bessel's inequality, orthogonal polynomials and completenessApproximation tools
– Fourier series, application of Parseval's identity, Discrete Fourier Transform, FFT
– Shannon-Nyquist Sampling Theorem, sinc functions
– Mallat's multi-resolution analysis (MRA), scaling function and wavelets, two-scale relation, Haar wavelets, Daubechies wavelets
– Finite elements, spline spaces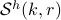 and B-splines
and B-splines 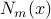 , finite element method for boundary value problems
, finite element method for boundary value problems
Linear operators and integral equations
– Bounded operators: norms of linear operators, unbounded operators, continuous linear functionals, spaces associated with operators, projection theorem
– Integral equations: Hilbert-Schmidt kernels, Fredholm kernel, Volterra Kernel
– Riesz Representation Theorem, adjoint of operators, weak form of a boundary value problem
– Compact operators: finite rank operators, approximation theorem, Hilbert-Schmidt operators, closed range theorem, Fredholm alternative theorem
– Spectral theory of compact operators: eigenvalues and eigenspaces, completeness of eigenfunctions, application of eigenfunctions in solving integral equationsDistributions and applications
– Test function space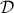 , distribution space
, distribution space 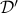 , Dirac
, Dirac 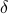 distribution, integral representation, derivatives of distributions
distribution, integral representation, derivatives of distributions
– Green's funtions and their applications
