Introduction to Random Dynamical Systems (AERO 630)

Basics of probability theory
     – Probability space and random variables
     – CDF and PDF, transformation rule, joint, marginal and conditional distributions and densities
     – Expectation and its properties, independence, conditional expectation, partition theorem, moments of a random vector: raw and central moments, correlation
     – Some inequalities: Cauchy-Schwarz, Holder, Jensen, Markov, Chebyshev
     – Moment generating function and characteristic function, Central Limit Theorem

Discrete-time stochastic process
     – Random sequences, i.i.d. and i.i.p. process and examples (Bernoulli process and 1D random walk)
     – Stationary, strictly stationary and wide-sense stationary (WSS) process
     – I/O description of linear system: causality, BIBO stability, DFT and convolution, response of discrete LTI system subject to WSS input, PSD and autocorrelation
     – White random sequence, ARMA model
     – Conergence of a random sequence: sure, almost sure, in probability, mean-square sense, in distribution; Law of large numbers: WLLN and SLLN
     – Markov chain on discrete state-space: transition kernel and probability, stationary distribution, homogeneous and inhomogeneous Markov chains, recurrent and
         transient states, positive and null recurrent states, aperiodic state, Perron-Frobenius Theorem and irreducibility condition, ergodicity, Doeblin decomposition,
         region-of-attraction (ROA), cell-to-cell mapping

Continuous-time stochastic process
     – Review of preliminary concepts: probability space,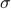 -algebra, probability measure, Borel 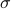-algebra, radom variable and its PDF, stochastic process
     – Dynamics of continous-time random variables, 1D Brownian motion, Ito-SDE, an example: Langevin equation for Duffing oscillator
     – Integration of SDEs, Ito version, Stratonovich version, strong and weak solution of SDEs
     – Different approaches for weak solution: statistical/equivalent linearization, moment closure, equivalent nonlinear equation, perturbation methods (e.g. WKB
        expansion) for low intensity noise, Markov methods
     – Markov methods: derivation of Chapman-Kolmogorov equation, Kramer-Moyal expansion, derivation of Fokker-Planck equation (Kolmogorov's forward
        equation) and its properties
     – Solving Fokker-Planck equation: stationary soluion: linear dynamics and Hamiltonian-like cases, rate-of-convergence to stationary solution, transient solution:
        numerical approach and curse-of-dimensionality